Prime-Free Regions

As I've already said on other pages, I'm a prime number junky.

Prime numbers are counting (whole) numbers which can't be divided evenly except by themselves or by the number 1.  So for example, the primes between 1 and 30 are:  2, 3, 5, 7, 11, 13, 17, 19, 23 and 29.  All the other numbers are evenly divisible by a previous counted number (other than 1).

I read somewhere that there were "arbitrarily large" consecutive spaces in the number series that contain no primes.  By "arbitrary" is meant any large number you care to name.  I found that rather hard to believe.  Primes are prolific and generally plentiful in any number range I've ever looked at -- up into the quadrillions, where my 1.8 MHz PC can still clank along (albeit slowly).  I'm no mathematician, so I can't fathom the deeper aspects of number theory.  Nor can I understand complicated math proofs.  But as an engineer I can appreciate data.  So I decided to develop some data sets which explore this notion of large "prime-free regions".

Let's set up a table that is 30 counting numbers wide, with each cell in the table representing a consecutive counting number.  Row 1 will have numbers 1 through 30, row 2 will be 31 through 60, row 3 will be 61 through 90, and so forth.  You'll find that after the first row, there are only 8 columns that contain prime numbers:  columns 1, 7, 11, 13, 17, 19, 23 and 29.  You can plot this 30-wide table graphically, lighting up the number cells that are prime.  Looking down through the resulting rows in this table, each row will have a certain number of prime cells illuminated.

Row 1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Row 2	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
Row 3	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90
Row 4	91	92	93	94	95	96	97	98	99		etc…
Row 5
Row 6

When you get down aways into the table, some rows will have no cells lit up -- which means that there were no numbers in the 30-wide row that were prime numbers.  The rest will have anywhere from 1 to 7 cells lit up.  (It's of some passing interest to find that no rows have all 8 "prime-active column" boxes lit up.  I don't know why that is, but I suspect it's an outcome of factor "sieve lines" that cross diagonally through the table.)  Since the frequency of prime numbers does indeed "peter out" somewhat as you go higher and higher (see note below), you'd expect that the "zero" rows would become more and more frequent as you go higher and higher in your count.  That is in fact the case.

Suppose we look at the ratio of prime number "hits" in consecutive 30-number blocks -- corresponding to each individual row in our modulo-30 number table -- relative to the number of 30-number blocks that have no hits at all.  That is, we'll calculate the ratio of the number of prime hits in all rows to the number of rows that have no hits.  We'll select a sizeable range of numbers (table size) to establish these ratios -- let's use ranges of 1,500,000 consecutive counting numbers -- 30-column tables that are 50,000 rows tall..

So here's the drill:  I look at the number of prime hits in each of the 30-number rows in my first 1,500,000-number table, then the next 1,500,000-number table, then the next, and the next, and so forth.  After getting these initial data on the first few tables, I can skip ahead to tables starting with much larger numbers -- making sure I keep the same modulo-30 order -- and do the same, up to (in my study exercise) 15,000,000,000.

In each table or "block" of 1,500,000 numbers, I interrogate a total of 50,000 rows (1,500,000/30).  I count the number of rows that have 0, 1, 2, 3, 4, 5, 6, or 7  primes lit up. Then I ratio those counts according to the "reference number" of the "0" row count.  I end up with the following data:

Start point (R=1.5 X 106)	0 Hits/0 Hits	1 Hit/0 Hits	2 Hits/0 Hits	3 Hits/0 Hits	4 Hits/0 Hits	5 Hits/0 Hits
1	1.0	3.7	5.6	4.4	2.10	0.54
1+1R	1.0	3.2	4.1	2.8	1.00	0.23
1+2R	1.0	2.9	3.6	2.3	0.87	0.17
1+3R	1.0	2.8	3.4	2.1	0.76	0.16
1+4R	1.0	2.8	3.3	2.0	0.69	0.14
1+10R	1.0	2.6	2.8	1.6	0.50	0.09
1+20R	1.0	2.5	2.5	1.3	0.41	0.07
1+50R	1.0	2.2	2.1	1.0	0.31	0.05
1+100R	1.0	2.1	1.9	0.9	0.25	0.03
1+200R	1.0	2.0	1.7	0.8	0.21	0.02
1+500R	1.0	1.9	1.5	0.7	0.16	0.02
1+1000R	1.0	1.9	1.4	0.6	0.13	0.018
1+10000R	1.0	1.6	1.1	0.4	0.07	0.010

You'll notice that all the 1, 2, 3, 4, and 5-hit ratios are declining relative to the "0" hit counts, given as a normalized reference.  (I've not shown the 6, 7 and 8 hit columns since 6 and 7 are miniscule ratios, and there are no rows at all with 8 primes in the "prime-active" columns.)

Let's plot the results graphically:

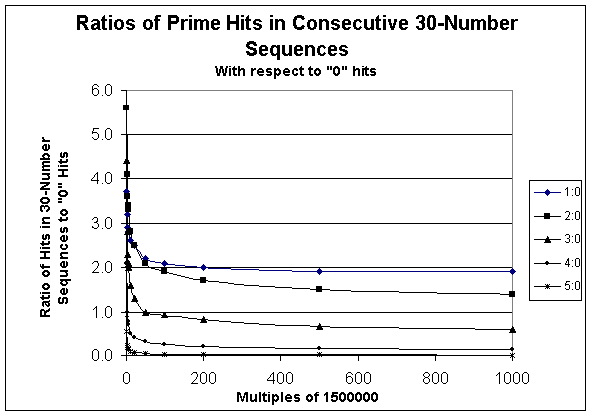
You can see that the ratios decline as we get higher and higher in the number series.  They decline fast in the early ranges and much slower later on.  To get a better handle on this, let's replot the chart on a logarithmic scale.  I'll just plot the 10X multiples of 1.5 million to make this a true "log-log" chart:

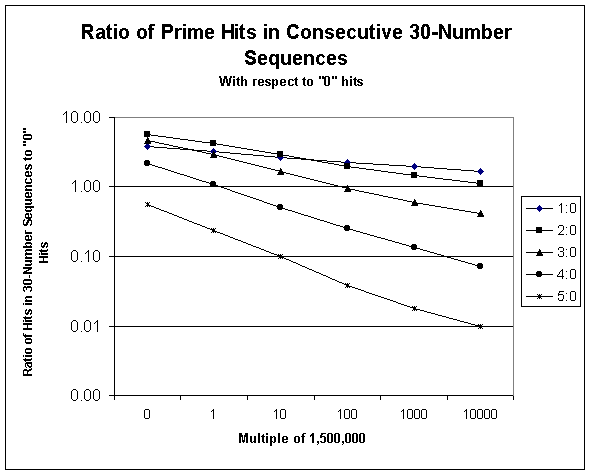
This is as cool as a snowcone at the South Pole!  The ratio lines descend in a straight-line fashion, plotted on a logarithmic scale.  Now, here's the thing:  Since the slopes of all the ratio lines are heading downwards, there must be a point somewhere along the far, far rightward portion of this graph where all the lines will eventually hit zero.  And if the ratios of the quantity of all the rows with prime hits to the quantity with zero prime hits become zero, then all 50,000 30-wide number rows in that interrogated range must have zero prime hits.  So at that far-distant point, there will be 1,500,000 consecutive numbers that contain no primes.  If I decide to bump that 1.5 million range up to a higher value, I'm sure that the same situation will apply.  And if I were a decent mathematician, I might even calculate (given the slope of the slowest-descending straight ratio line) the X-axis intercept point -- which would say exactly where on the number scale that prime-free region resides.

But wait a minute, not so fast.  I cheated on the logarithmic graph shown above.  The bottom line showing "0.00" is not really zero, but rather "0.001".  (You can't plot a log graph with a zero on the y-axis.)  I didn't show enough of the significant digits of the Y-axis numbers.  The true situation is as follows:

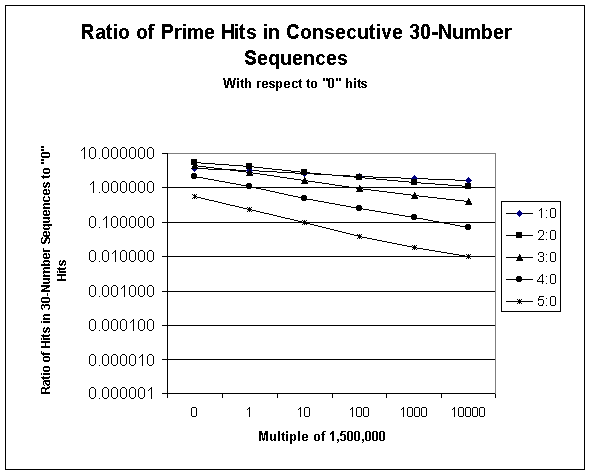
Based on this piece of information, I'm not really convinced that the sloping lines will ever hit true zero.  This appears to me to be somewhat like the paradoxes of Xeno:  If a downward sloping line ever does hit the "defined" X-axis, there will always be another lower number you can plug into the Y-axis scale to give it another ramp to fall through.  (This is actually another way of showing that there are no "end" to the prime numbers.)

But let's think about this some more.  While we are talking about ratios (very small ones, as we get out into the nether regions of numbers), the original subject at hand was whole counts.  If the ratios get so small that they aren't reflective of the counts in question, then they essentially become zero.  For example, if the miniscule ratio is extrapolated to be 1 "row hit" in one million (the lowest line on the above log graph), and you are only talking about 50,000 total row counts in the first place, then that axis line can certainly be considered "less than zero", right?   For 50,000 numbers, any ratio less than 0.00002 (equal to 1 row hit out of 50,000) is, for all intents and purposes, zero.  So we should set that Y-axis line as the point at which zero prime hits is achieved.

So I've managed (at 6:13 am, after a long night of thinking) to salvage my original project.  There are truly large (at least 1,500,000 long) prime-free regions, somewhere out there in the stratospheric areas of the number series.  I would shout for joy, would it not be for the fear of waking up Chris...

 

   Back to Prime Number Explorations...  

While the frequency of primes diminishes as the numbers get higher, they never quit.  Euclid proved that there are infinitely many prime numbers.  Furthermore, Carl Friedrich Gauss (in 1792) showed that the quantity of primes less than the number n can be approximated by the function n/log n.  He was only fifteen at the time.  Smart kid!  Looked at another way, if you pick a number at random between 0 and n, the odds of it being prime are about 1/log n.

I referred to diagonal "factor sieve lines" above.  The selection of the table modulus (30 wide) was not arbitrary on my part.  If you establish the table width as a multiplicand of the first few primes, then the subsequent "prime-active" columns become vertical.  If you think about this, it makes sense.  In this case, 30=2X3X5.  Every 2nd column is divisible by 2, every 3rd column by 3 and every 5th column by 5.  That leaves only 8 columns out of the 30 that can potentially be prime.  But since the next prime factor, 7, doesn't divide evenly into 30, its multiplicands aren't arranged in a vertical row, but rather in a diagonal fashion.  You can identify those 7-factorable cells by doing a "knight's move", beginning with the 7-factorable numbers in the first row  -- 7, 14, 21, or 28.  If you move down one and left two from any of those cells, you'll run into a number divisible by 7.   Alternately, you can go the other way, one down and 5 right to establish the same diagonal lines.  All the multiplicands of other, higher prime factors can also be plotted on their own unique diagonal "sieve lines".   (For example, for the next prime factor 11, an 11-divisible number is found on the diagonal defined by going one down and 8 left from any number divisible by 11, or one down and 3 right, whichever you prefer.)  I think it's the "7" factor sieve lines that foil any chance of having all 8 "prime-active" columns in this mod-30 table from being lit up.  How to prove that, I leave to "real" math folks.  If you imagine all these countless "sieve lines" running through the table, you can begin to appreciate that the prime numbers represent the "holes" in the overall factoring net -- in this sense, they are defined as what they aren't, rather than what they are -- the nothingness embedded in the somethingness.  And that is why I'm drawn to them!

In case you were wondering, the frequency of primes found in any of the 1st, 7th, 11th, 13th,  17th, 19th, 23rd,  or 29th "prime-live" columns in this 30-mod table is exactly the same as in any other of the "prime-live" columns.  That is, the distribution of primes across these columns is absolutely flat.  So it's no real surprise, given young Master Gauss's finding, that each of the above ratio lines obeys a logarithmic "declining" pattern.  Any one of these "prime-rich" columns simply recapitulates the situation you would get with a table only one column wide, containing all the whole numbers listed in it sequentially.  The frequency of primes in 10X-sequential large segments of a mod-1 table should also obey a straight logarithmic function like the lines shown above.  (It does -- I just this minute verified it.)

My aching brain doesn't want to do the math required to calculate the exact X-axis intercept (i.e., with Y=0.00002) on a log scale, using the lowest sloping line in my above graph.  However, by just projecting the straight lines on an extended chart like the one above, I would reckon that my 1,500,000 consecutive prime-free region begins at around N=10⁵⁶, or:

     100,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

This isn't too awfully far off from the total number of atoms contained in the Universe, which has been estimated at 10⁶³.  Alas, I don't have several lifetimes to devote to verifying my N projection using my PC.  While that number might seem pretty large, it pales to insignificance in the world of "largest primes discovered".  In March 2005, a prime number was discovered (a "Mersenne Prime") that was 2^25,964,951-1.   It has 7,816,230 digits, and if printed out in its entirety, would fill 235 newspaper pages!  I think prime numbers must truly be very sparse out in that neighborhood...